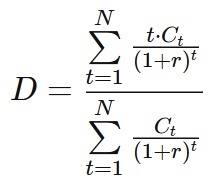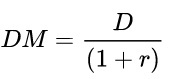Durata finanziaria di un titolo obbligazionario (duration): cos’è e che informazioni ci dà?

Quando pensiamo ai mercati obbligazionari spesso li consideriamo come un investimento più sicuro rispetto all’azionario. Ma anche l’acquisto di titoli a reddito fisso (come i Bot o i Btp) presenta dei rischi (se volete approfondire la tematica vi consiglio questo mio vecchio articolo: Le azioni sono sempre più rischiose delle obbligazioni?). 

Uno dei principali rischi di un titolo, insieme al rischio di default dell’emittente (quindi al mancato pagamento delle cedole e il rimborso del capitale a scadenza) è rappresentato dal rischio di tasso. Con questa tipologia di rischio si fa riferimento alla possibilità che una variazione dei tassi di interesse riduca il valore delle cedole e/o del rimborso a scadenza.

Questo rischio è legato alla relazione che esiste tra prezzi e i tassi di interesse. Queste due variabili, infatti, si muovono sempre in direzione opposta:

• un rialzo dei tassi provocherà una discesa nel prezzo delle obbligazioni;
• un ribasso dei tassi provocherà un apprezzamento delle obbligazioni.

(se volete capire il motivo queto comportamento potete approfondire con questo vecchio articolo: Perché l’aumento dei tassi fa scendere il prezzo delle obbligazioni?)

In prima battuta si potrebbe pensare di misurare il rischio di tasso calcolando la durata di un impiego obbligazionario in termini di quanti giorni mancano al rimborso del valore nominale del titolo, in altre parole la vita residua dell’obbligazione. All’estrema semplicità di calcolo e di interpretazione si contrappone però una valenza pratica molto scarsa, visto che non tiene conto della diversa manifestazione nel tempo di tutti i flussi di cassa generati dall’investimento, a partire dalle cedole. 

Un’altra misurazione, invece, che risulta molto più utile in termini pratici è la durata finanziaria dell’obbligazione, o meglio conosciuta come “duration”.

La duration: cos’è e come funziona

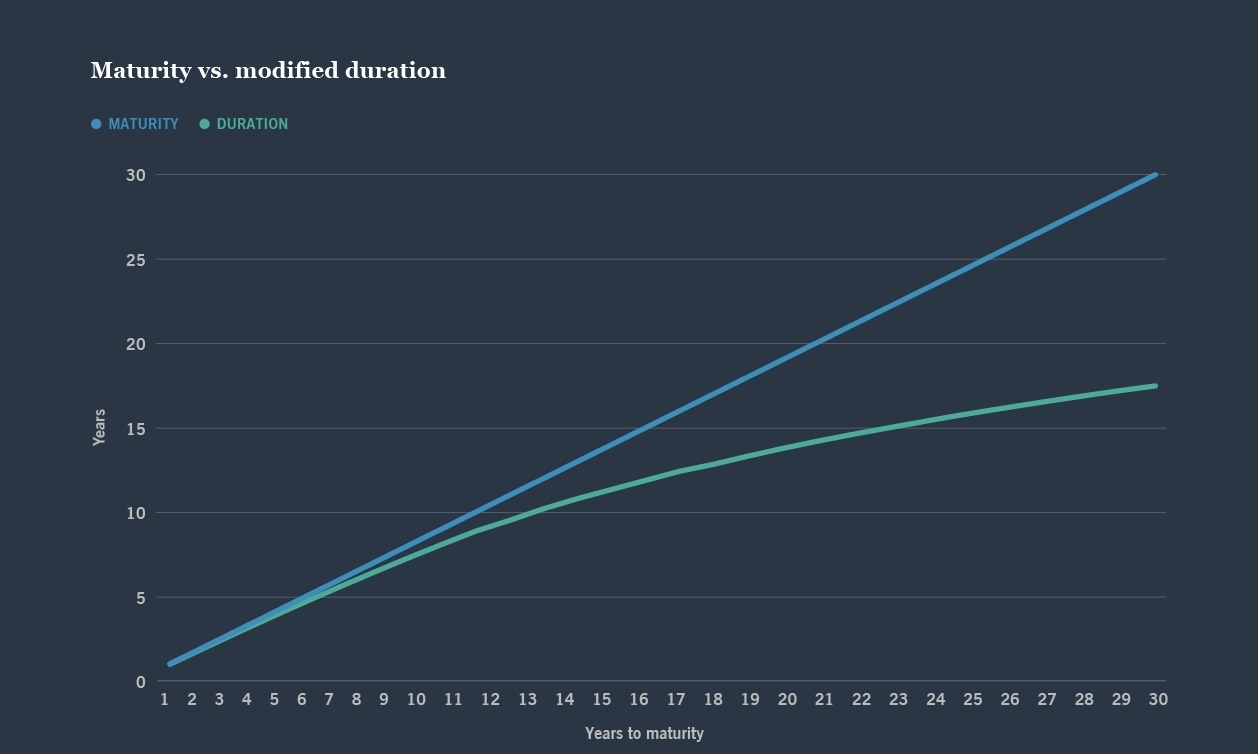
La duration, o durata finanziaria di un titolo, viene definita come durata media finanziaria di uno strumento finanziario. Nel Grafico 1 possiamo notare come duration e visa residua siano due concetti distinti che si comportano in modo differente in funzione del tempo a scadenza.  La duration si può configurare come la sensibilità di un'obbligazione o di un portafoglio obbligazionario alle variazioni dei tassi d'interesse e viene calcolata come media ponderata delle scadenze dei flussi di cassa da esso generati, nella quale i pesi sono dati dai rapporti tra i valori attuali dei flussi ed il prezzo corrente di mercato dello strumento.

Grafico 1: Maturity vs Duration Modificata

Fonte: Securities Evaluations Inc

I significati che questo indicatore può assumere sono quindi molteplici e vanno dal “periodo necessario per rientrare dall’investimento effettuato” al “il periodo per il quale si è esposti al rischio dai tasso di interesse”.

La duration è comunemente conosciuta come un indicatore importante per gli investitori poiché consente loro di valutare il rischio di tasso di interesse associato ai titoli obbligazionari e di gestire il proprio portafoglio in modo efficiente, bilanciando la sensibilità ai tassi di interesse con altri obiettivi di investimento. La duration viene considerata anche come una misura approssimativa della volatilità di un titolo obbligazionario. Una duration più lunga indica una maggiore sensibilità ai cambiamenti dei tassi di interesse, mentre una duration più breve indica una minore sensibilità. Per questo motivo la duration è nota per essere una misura per valutare utilizzata nei mercati obbligazionari per valutare i rischi connessi a eventuali cambiamenti dei tassi d’interesse.

Compito principale della duration è uniformare il calcolo della durata di ogni obbligazione a quella che sarebbe se la stessa fosse del tipo zero coupon, in modo da poter effettuare paragoni omogenei. Per esprimere la variazione percentuale nel prezzo di un titolo di debito in risposta a una variazione unitaria dei tassi di interesse, si moltiplica la duration per la variazione percentuale dei tassi di interesse. 

Le variabili che impattano maggiormente la duration

Per comprendere i principi basilari d’impiego della duration si possono evidenziare le seguenti caratteristiche:

1. è inversamente proporzionale al coupon rate: se due Btp sono identici per caratteristiche con l’eccezione del tasso di rendimento cedolare, il titolo con un coupon rate minore avrà una duration più elevata. In altre parole, la duration è inversamente proporzionale al coupon rate;
2. è dunque direttamente proporzionale alla scadenza: se due Btp sono identici fuorché per la scadenza, quello con scadenza maggiore avrà duration più elevata;
3. è inversamente proporzionale al rendimento a scadenza (yield to maturity): se due Btp sono identici con l’eccezione del rendimento a scadenza, quello con rendimento a scadenza maggiore avrà duration minore. 

Infine in caso di assenza di cedole la duration corrisponde alla vita a scadenza del bond (un esempio è un bond zero-coupon come Bot o un Ctz), ossia non distribuisce cedole, la duration dell’obbligazione corrisponde alla vita a scadenza del titolo (time to maturity).

A questo punto però può sorgere spontanea la domanda: come applicare a livello pratico questi concetti? Bene dobbiamo introdurre il concetto di duration modificata. La duration modificata viene calcolata a partire dalla duration che viene poi divisa per il tasso di rendimento attuale del titolo (questo rappresenta il tasso che ci consente di eguagliare il prezzo pagato per acquistare un titolo di debito con la somma dei valori attuali di tutti i flussi futuri, sia in linea interessi che in linea capitale, che maturano a beneficio del possessore; parlando in termini pratici è una sorta di “tasso completo a scadenza”).

La duration modificata funge da moltiplicatore del movimento dei tassi di interesse. In pratica, la duration modificata ci permette di calcolare la variazione percentuale del prezzo di un titolo nell’ipotesi di un movimento parallelo e istantaneo dei tassi.
Un esempio ci aiuta a semplificare la definizione: se i tassi d’interesse dovessero salire da 3% a 5% il nostro titolo obbligazionario subirebbe una perdita tanto maggiore in funzione della sua duration. Un titolo con duration 10 (dove 10, lo ricordiamo, è un periodo di tempo) avrebbe una perdita maggiore di un titolo con duration 6. Viceversa, se i tassi dovessero da 5% scendere a 3% il maggior guadagno lo avremo sul titolo con la duration maggiore.
Se per esempio la duration modificata è 5, significa che al rialzo/ribasso di un 1% nei tassi di mercato il prezzo del tuo bond scenderà/salirà del 5%.

Come si calcola: formula ed esempio pratico

La duration si ottiene calcolando la media ponderata delle scadenze temporali in cui saranno incassate le cedole e verrà rimborsato il capitale.

Può essere tradotta come la durata media finanziaria. Viene espressa in anni e giorni; ad esempio, una duration di 5,11 sta a significare 5 anni e 40 giorni. 

Dove:

• t è il tempo a scadenza
• t *   è il flusso di cassa che l’investimento genera
• r è il tasso di rendimento effettivo a scadenza

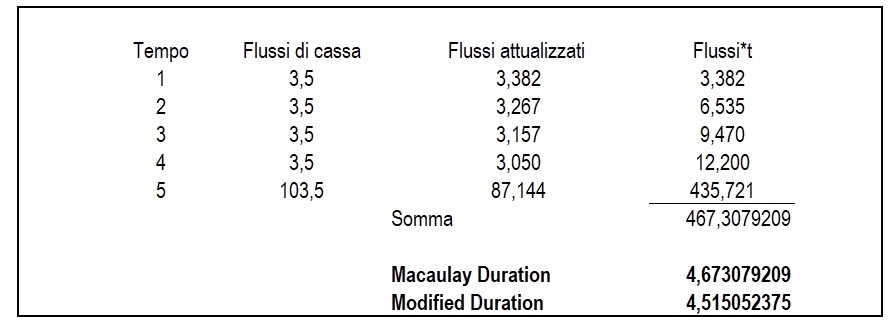
Facciamo un esempio pratico; immaginiamo di avere un titolo Btp con durata 5 anni, emesso a 100, cedola annua 3.5%, rimborso unica soluzione alla scadenza, tasso di rendimento effettivo a scadenza 3.5% (essendo emesso alla pari, cedola e Tres coincidono).

I passaggi per calcolare la duration i seguenti:

1. Calcolare i flussi di cassa attualizzati: flusso di ciascun anno / (1+tres)^t;
2. Moltiplicare i flussi per la durata: per il primo anno flusso attualizzato per 1, per il secondo anno flusso attualizzato per 2, e così via;
3. Sommare i risultati;
4. Dividere per il prezzo;
5. La duration modificata si determina dividendo la duration per (1+ il rendimento effettivo del bond).

Una duration modificata pari a 4,5150 significa il prezzo del Btp in caso che di rialzo/ribasso di un 1% nei tassi di mercato il prezzo:

• Scenderà del 4,5150% se i tassi aumenteranno dell’1%
• Aumenterà del 4,5150% se i tassi scenderanno dell’1%

Conclusioni: riflessioni finali

L’impiego della duration nella gestione di un portafoglio di titoli obbligazionari è fondamentale, proprio perché eventuali variazioni dei tassi d’interesse possono tradursi in forti perdite. 

Gli investimenti in titoli che hanno duration più lunghe sono più sensibili al rischio collegato alle eventuali variazioni dei tassi d’interesse, mentre quelli con duration più brevi tendono a essere più immuni da questo pericolo.

La duration può rivelarsi uno strumento estremamente utile per i gestori obbligazionari nella costruzione dei portafogli e nella gestione del rischio. Con il mutare delle prospettive economiche, il gestore può variare la duration media del portafoglio obbligazionario in funzione degli obiettivi d'investimento.

Al momento di decidere quali obbligazioni acquistare, gli investitori dovrebbero considerare la propria tolleranza alla volatilità e le proprie convinzioni in ordine alla futura direzione dei tassi d'interesse. Gli investitori che nutrono un'avversione al rischio o che temono oscillazioni significative nel valore delle loro partecipazioni dovrebbero valutare una strategia obbligazionaria con duration più breve. Analogamente, si potrebbe utilizzare il concetto di duration per adottare una strategia attiva di investimento:

• Quando ci si aspetta una salita dei tassi è opportuno ridurre la durata media dei bond;
• Quando ci si aspetta una discesa dei tassi si aumenta la duration del portafoglio.

L’impiego della duration nella gestione di un portafoglio di titoli obbligazionari è fondamentale, anche perché la sua sensibilità a eventuali variazioni dei tassi d’interesse può tradursi in forti perdite. Basti pensare che una crescita di qualche punto % su un titolo di stato a lunga scadenza impatti molto negativamente. 

Va infine detto che la duration è un ottimo indicatore di stima del rischio di tasso ma al tempo stesso non completo. La duration costituisce una buona stima della relazione esistente tra prezzo e rendimento di un’obbligazione solo in corrispondenza di variazioni infinitesime del rendimento, dal momento che si basa su un’approssimazione lineare della curva prezzo-rendimento. L’errore che si commette, come possiamo notare nel Grafico 3, è pari alla distanza verticale tra la retta tangente alla curva e la curva stessa.
Per migliorare l’accuratezza della stima fornita dalla duration della variazione del prezzo di un'obbligazione al variare del rendimento della stessa, si considera il grado di curvatura (la convessità) della curva prezzo-rendimento. Sulla base della convessità si definisce un termine aggiuntivo da inserire nell’espressione che approssima la variazione del prezzo di un titolo obbligazionario al variare del rendimento.

Resto a disposizione per qualsiasi dubbio o domanda.